Simulation of Laminar Compressible Flows

The Stream solver can simulate flows where compressible effects are present, including flows with shock waves. Compressibility of a flow is usually categorized by observing a change of the density of a fluid as a response to a change in the pressure. Compressibility should be considered where flows may have Mach numbers greater than 0.3 typically. Another class of flows that should be solved by considering compressibility effects are Rayleigh-type flows where heat transfer through boundaries is considered.

For compressible flows without shock waves, the user should use the FOU and SOU flux schemes. For flows with shock waves, the SLAU flux scheme is available. Details about the flux schemes that are available in are detailed here. The run control file specification mostly remains the same from incompressible cases. An additional data file, called a chemistry model file(.mdl), is required for compressible flows. See the following Appendix contains more information about the contents of a chemistry model file and information about how to create one.

Example Case: Prandtl-Meyer Fan

Consider the case of a compressible laminar inviscid flow around a corner as shown below. For this case, the fluid in the domain is air. Details about the problem and grid and run control file can be found on our website. In this example, a flow of air at a temperature of 550 Rankine (305 Kelvin) moving at Mach 2.5 flows past a bend in the geometry of the domain. The supersonic flow produces a Prandtl-Meyer expansion fan near the corner in response to the bend.

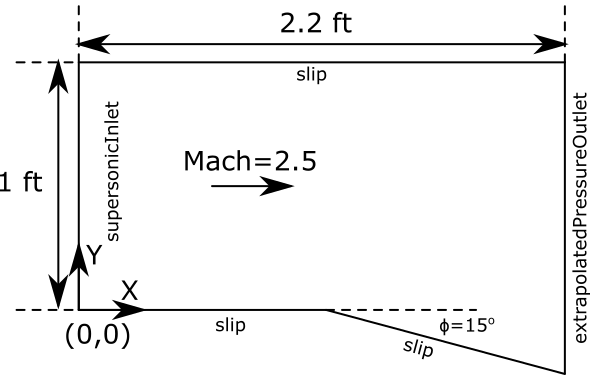
Domain diagram for the Prandtl-Meyer expansion fan problem.

A sample run control file used to run the Prandtl-Meyer simulation is shown below.

Sample run control file for the Prandtl-Meyer expansion fan problem.

{
grid_file_info: <file_type=VOG, Lref=1m, pieSlice>

boundary_conditions: <
Inlet=supersonicInlet(v=2874 ft/s, p=12 psia, T=550 R),
Outlet=extrapolatedPressureOutlet,
Wall=slip,
Top=slip,
BC_5=symmetry(),
BC_6=symmetry()
>

initialCondition: <T=550 R, p=12 psia, v=2874.0322 ft/s>

// Flow properties
flowRegime: laminar
flowCompressibility: compressible

// Gas Model & Transport Properties
chemistry_model: air_1s0r
transport_model: const_viscosity
mu: 1.0e-15
kcond: 1.0e-15

// Time-Stepping
timeIntegrator: BDF2
timeStep: 1.0e-5
numTimeSteps: 10001
convergenceTolerance: 1.0e-30
maxIterationsPerTimeStep: 30

// Fluxes
inviscidFlux: SOU
limiter: venkatakrishnan

hypreSolverName: GMRES
linearSolverTolerance: 1.0e-02

// Momentum equation (linearSolver[SGS], 0.0<relaxationFactor<1.0)
momentumEquationOptions: <linearSolver=SGS,relaxationFactor=0.5,maxIterations=5>

// Pressure equation (linearSolver[SGS, PETSC, HYPRE], 0.0<relaxationFactor<1.0)
pressureCorrectionEquationOptions: <linearSolver=HYPRE, relaxationFactor=0.1, maxIterations=50>
pressureBasedMethod: SIMPLEC

// Energy equation (linearSolver[SGS], 0.0<relaxationFactor<1.0)
energyEquationOptions: <linearSolver=SGS, relaxationFactor=0.3, maxIterations=5, form=temperature>
TclipMax: 2000.0

// Printing, plotting and restart parameters.
print_freq: 100
plot_freq: 500
plot_output: pResidualTT
restart_freq: 1000
}

Boundary Conditions

The boundary condition used for the inflow in this case is the supersonicInlet. This boundary condition is used for flows with Mach numbers greater than one. The velocity, pressure, and temperature must be specified for this inlet. The velocity specification v= assumes that the velocity is directed along the normal vector pointing into the domain. See the following Appendix for more information about all the ways to provide specifications to this boundary condition.

Inlet=supersonicInlet(v=2874.0322 ft/s, p=12 psia, T=550 R)

For supersonic flows, the location of the outlet boundary can be much closer to the area of interest because disturbances near the boundary do not travel back into the domain due to the supersonic nature of the flow. The outlet boundary is located just downstream of the corner in this example and is an extrapolatedPressureOutlet. This boundary condition is a zero-gradient boundary that is permissible in the presence of flows that are supersonic.

Outlet=extrapolatedPressureOutlet

All solid surfaces are set to the slip boundary condition because of the inviscid nature of the flow. The front and back (going into the page) boundaries are set to symmetry to model zero variation in the flow field in the z-direction.

Initial Conditions

In this example the initial flow is air in motion with a velocity of 2874 ft/s. The pressure is 12 psia and the temperature is 550 Rankine. These initial conditions are specified as follows:

initialCondition: <v=2874 ft/s, p=12 psia, T=550 R>

English units are used in this example to show that different unit types are supported for many of the inputs. All inputs are converted to S.I. units within the code.

Transport Properties

For this case, the fluid is air, and the viscosity is set to a small value to approximate an inviscid flow. The thermal conductivity is also provided for use in the energy equation.

transport_model: const_viscosity

mu: 1.0e-15

kcond: 0.0265

A specification of the species that are present in the domain is needed when running compressible flows. This provides information about the equation of state to use for the species. The species information for the air is encoded in the chemistry model file (.mdl), which has its specification provided here. The contents of the file are reproduced below for ease of replicating this case.

The .mdl file for the air species used in the Prandtl-Meyer expansion fan case.

// Model for Air as an ideal gas
species = {
_Air = < m=28.89, n=2.5, href=0, sref=0, Tref=298.0, Pref=10000.0, mf=1.0 >;
};
reactions = {
};

Numerics

The first-order accurate BDF time-stepping scheme is used for this case because we are primarily interested in the steady-state behavior of the expansion fan within the domain. The second-order inviscidFlux option SOU are used is used because of its low numerical dissipation characteristics. For supersonic flows with shockwaves, the SOU flux scheme is not appropriate because it is unstable in the presence of discontinuities in a flow, but it is ok for this case because there is only a smoothly varying isentropic expansion fan in the domain for this case.

The momentum, pressure correction, and energy equations need to be solved for compressible laminar flows. The specification for the momentum equation options is shown below. Here we are using the symmetric Gauss-Seidel (SGS) method to solve the linear system. A relaxation factor of 0.5 has been chosen, which indicates the 50% of the current iteration solution and 50% of the previous iteration solution will be averaged and used as the new value. Lower values for the relaxationFactor can be used if numerical stability issues arise. The maxIterations option specifies the maximum number of iterations to use in the linear solver. For the SGS solver, the maximum number of iterations is always used. Typically, one should not use more than 5 iterations in the linear solver for the momentum equation.

momentumEquationOptions: <linearSolver=SGS, relaxationFactor=0.5, maxIterations=5>

Options for pressure-correction equation are shown below. The PETSC linear solver is used in this case to show that other linear solvers are supported. Typically, more iterations are required for the pressure-correction equation than the other governing equations.

pressureCorrectionEquationOptions:<linearSolver=PETSC, relaxationFactor=0.5,maxIterations=5>

For compressible flows Stream supports three forms of the energy equation: a temperature form, a total energy form, and a total enthalpy form. For this case, the temperature form of the energy equation is used by specifying form=temperature in the energyEquationOptions. The other forms of the energy equation are discussed in the Appendix.

energyEquationOptions: <linearSolver=SGS, relaxationFactor=0.3, maxIterations=5, form=temperature>

Miscellaneous

In Stream, an inviscid simulation can be approximated by setting the transport_model variable to const_viscosity and providing a very small value of the viscosity, as was done in this example.

Helpful Guidance

• The table below shows additional field variables that are available for output in laminar compressible flow simulations. These are in addition to the field outputs that are available for the laminar incompressible simulations. Default variables are output automatically and do not need to be specified in the plot_output line in the run control file. The variables pResidualTT and vResidualTT shown in the table are useful for gauging solution convergence. A discussion of the principle behind the turn-over time can be found here.

Field Variable Output for Laminar Compressible Flows

Variable	Description	Default
a	Speed of sound	Yes
cfl	CFL number	No
cp	Specific heat	No
kineticEnergy	Kinetic energy	No
hResidual	Energy eq. residual	No
hResidualTT	Energy eq. turn-over time	No
kconduct	Thermal conductivity	No
mix	Species mass fractions	Yes
t	Temperature	Yes