Simulation of Turbulent Flows

In this section, we describe the capabilities within Stream for simulating turbulent flows. Stream contains a variety of turbulence models that are suitable for both steady-state and unsteady turbulent flow analysis. Here we assume that the user has a sufficient understanding of the terminology used in the description of turbulent flows and knowledge of the various analytical turbulence closure models that are employed in the CFD field. For a more comprehensive description of the governing equations of turbulent flow and the specific turbulence models used in Stream, see [Pope2000] as well as the Stream Theory Manual.

RANS Models

Stream contains a selection of Reynolds-Averaged Navier-Stokes (RANS) turbulence models from both the k-epsilon and k-omega families. The governing assumptions behind the derivation of these models generally limits their accurate predictive capability to relatively benign turbulent flow scenarios in which flows remain predominantly attached to the walls of the domain (no separation). Mean-flow properties of separated flows (such as drag coefficients) can be accurately predicted, including for flows with massive separation under certain conditions (i.e., post-transition, supercritical turbulence), however, the prediction of intermittent and transitional behavior of flows cannot be predicted with these models. The paper of Hart [Hart2016] contains a detailed comparison of RANS turbulence models and Scale Resolving Simulation (SRS) models (which includes the DES and LES models to be discussed later in this chapter), regarding their predictive capability for massively separated flow. This information may be of use in helping users decide whether RANS models are applicable to their problems of interest.

One major addition to the run control file for turbulent flow is the variable turbulenceEquationOptions. This variable is used for specifying the turbulence model, the relaxation and linear solver parameters for the turbulence equations and any other auxiliary input required by the turbulence models. Turbulence model selection is made using the model option. The table below shows the allowable values for this option for RANS simulations.

Freestream values for the turbulence variables may be set using the kFreestream, omegaFreestream and epsilonFreestream variables. These variables are commonly set to the same values that have been specified at the inlet boundary and have default values of 1.0e-08, 10.0 and 10.0, respectively. These variables are only used to ensure that the computed turbulence values remain realizable (i.e. k, omega, epsilon > 0) and will have no impact on the final solution unless clipping of the turbulent variables is occurring.

RANS Turbulence Model Options for `turbulenceModelOptions` variable
Model Family	Model Names	Notes
k-\(\epsilon\)	`StandardKE` `RealizableKE`	`StandardKE` from Launder & Spaulding [LaSp1974] `RealizableKE` model of Shih et. al. [SLSY1995]
k-\(\omega\) BSL	`menterBSL` `menterBSL_m` `menterBSL_V` `menterBSL_Vm` `menterBSL_KL` `menterBSL_KLm`	`menterBSL` is the original 1994 Baseline Model of Menter For other variants of the Menter baseline models, see NASA BSL
k-\(\omega\) SST	`menterSST` `menterSST_m` `menterSST_V` `menterSST_Vm` `menterSST_KL` `menterSST_KLm`	`menterSST` is the original 1994 Shear Stress Transport Model of Menter For other variants of the 2003 Menter shear-stress transport model, see NASA SST
k-\(\omega\)-SST-2003	`menterSST2003` `menterSST2003_m` `menterSST2003_V` `menterSST2003_Vm` `menterSST2003_KL` `menterSST2003_KLm`	`menterSST2003` is the improved 2003 Shear Stress Transport Model of Menter For other variants of the Menter shear-stress transport model, see NASA SST

DES Models

While the RANS models described above may be used in an unsteady mode with small time step to simulate complex turbulence flows with separation and bluff-body-type recirculation zones, they are generally found to be lacking for these flows. Typically, in zones of separation, one expects to find a collection of eddies that span a range of length scales, from the largest energy-containing eddies to the smallest dissipative eddies of the turbulence cascade. However, due to the modeling assumptions made during closure of the ensemble-averaged equations, solutions for separated flows are almost universally found to exhibit a time-averaged character, whereby small-scale eddy content is severely diminished or even completely absent, and the point-by-point frequency spectrum is devoid of any chaotic or high-frequency content. To provide a remedy for this deficiency, Stream provides several turbulence models in the Detached-Eddy Simulation (DES) family, which can be used to simulate turbulent flows with significant separation. While the analytical formulation these models is not based on the strict filtering process used in the traditional Large-Eddy Simulation (LES) approach, these DES models provide turbulent solutions that are similar in character to LES models and are thought of most conveniently as hybrid models that blend the characteristics of LES in separated an interior region while transitioning to traditional Unsteady RANS (URANS) behavior in the near-wall region. A great discussion about detached eddy simulation methodology can be found here.

A Brief DES History

A brief history of DES family of models is presented below for readers who may be interested in the evolution of the DES models.

History of DES Family of Models
Reference	Main Features	Comments
Spalart 1997	Original motivation for DES Basic equations (with \(C_{des}\) constant undetermined) Two-dimensional examples.	First paper on DES concept In the context of Spalart-Almaras (SA) model only
Shur 1999	First true 3D application of DES Calibration of \(C_{des}\) Successful prediction of airfoil forces	Usage of DES in 3D
Travin 2000	First DES with grid refinement Fair agreement on the drag crisis Refined definition of DES
Nitkin 2000	Discussion of DES for wall modeling inside LES	One of the first attempts of employing DES as an LES using wall modeling
Strelets 2001	Wide range of applications, including models other than Spalart-Almaras.	First SST-DES formulation
Menter and Kuntz 2002	Demonstrate grid-induced separation Propose shielding for SST model to “preserve RANS mode” or “delay LES mode” in boundary layer by using blending functions \(F_1\) or \(F_2\)	First demonstration of Grid-Induced Separation (GIS) with DES They refer to it as “Zonal SST-DES” Ambiguity in “shielding” function - can use \(F_1\) or \(F_2\) → Spalart 2006 improves this Provides motivation for the DDES model of Strelets (2006)
Spalart 2006	Introduced Delayed DES (DDES) to avoid grid-induced separation (GIS) Coined the phrase Modeled-Stress Depletion (MSD) and showed it to be the cause of GIS Use more generic shielding function based on eddy viscosity and wall distance (using parameter \(r_d\) and function \(f_d\))	MSD results from insufficient flow instabilities downstream of the switch from the RANS to the LES model formulation => the switch from the RANS to the LES model inside wall boundary layers is not desirable Applied to S-A model in this paper But also applicable to SST model (done in Gritskevich-Menter 2012)
Shur 2008 & Travin 2006	Improved DDES (IDDES) Combines DDES with an improved hybrid RANS-LES aimed at Wall-Modeled LES (WMLES) Uses rather intricate blending and shielding functions Has 2 branches: DDES and WMLES	Original DES results in a strong Logarithmic Layer Mismatch (LLM) between the inner RANS and the outer LES regions IDDES aims at a true WMLES capability: resolves the LLM issue by using subgrid length-scale which depends not only on the grid spacings but also on the wall distance
Gritskevich & Menter 2012	Modifications to DDES and IDDES for SST model SST-DDES: Recalibrated empirical constants of DDES (Spalart 2006 which was calibrated for S-A model) for the SST model SST-IDDES: modified IDDES (of Shur 2008) which is more suitable for SST model	Can consider SST-IDDES as a viable Wall-Modeled LES (WMLES) which is valid in the entire flow - boundary layer, attached flow regions and separated flow regions → cover only the inner-most part of the boundary layer in RANS mode and resolve most of the turbulence inside the boundary layer by LES

Activating DES Mode

To active DES mode in Stream, the user should provide an addition option in the turbulenceEquationOptions options list of the form des=<ModelName>. An example is shown below.

turbulenceEquationOptions: <model=menterSST2003, des=IDDES2012, linearSolver=SGS, relaxationFactor=0.5, maxIterations=5>

The table below shows the allowable values for the des option for running simulations with DES.

DES Turbulence Model Selection for `turbulenceModelOptions` variable
Model Value	Description
`DES2001`	2001 Strelets DES model [Stre2001]
`DDES`	Menter Delayed DES model [MeKu2002]
`DDES2012`	2012 SST-DDES model [GGSM2012]
`IDDES2012`	Improved 2012 SST-IDDES model [GGSM2012]

A recommended combination is the menterSST2003 turbulence model with the IDDES2012 des model. For cases that experience numerical instability, try the DDES2012 des option.

Example Case: Backward Step

Consider the case of a compressible turbulent flow over a backward step as shown in Figure 8. For this case, the fluid in the domain is air. Details about the problem and grid and run control file can be found on our website.

In this example a turbulent flow of air at around 537 Rankine (298 Kelvin) is moving at 41.7 m/s and it passes over a sudden drop. This drop causes the flow to create a circulating region near the drop. The size and character of this recirculation bubble is the subject of the backward step problem. The RANS solution of the flow field is what will be solved for in this example.

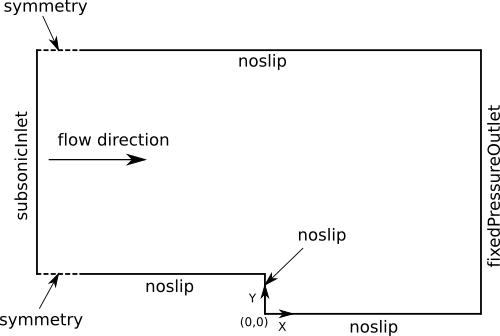
../_images/backward_step_domain.png — Domain diagram for the backward step problem.

When running turbulent simulations, most of the run control file inputs described in previous chapters remain the same, with minor changes. Some additional input required for the specification of data needed for the governing turbulence equations is required. A sample run control file used to run the backward step simulation is shown below.

Sample run control file for the backward step problem.

{
grid_file_info: <file_type=VOG, Lref=1m, pieSlice>

boundary_conditions: <
BC_1=noslip(adiabatic), //Upstream Bottom Wall
BC_2=noslip(adiabatic), // Top Wall
BC_3=subsonicInlet(T=537.0 R, v=41.7096 m/s, k=0.00097, omega=5091), //Inlet
BC_5=symmetry, //Backwall
BC_6=symmetry, // Frontwall
BC_13=noslip(adiabatic), // Bottom of Downstream section
BC_15=noslip(adiabatic), // Vertical Step Face
BC_22=fixedPressureOutlet(pMean=1.0 atm), // Outlet
>

initialCondition: <p=1 atm, T=537.0 R, v=41.7096 m/s, k=0.00097, omega=5091>

// Flow properties
flowRegime: turbulent
flowCompressibility: compressible

// Gas model.
chemistry_model: air_1s0r
transport_model: const_viscosity
mu: 2.498e-5
kcond: 4.175e-2

// Time-stepping
timeIntegrator: BDF
timeStep: 1e-3
numTimeSteps: 10001
convergenceTolerance: 1.0e-30
maxIterationsPerTimeStep: 30

// InviscidFlux
inviscidFlux: SOU
turbulenceInviscidFlux: SOU
limiter: venkatakrishnan

linearSolverTolerance: 1.0e-02

// Momentum equation (linearSolver[SGS,PETSC],0.0<relaxationFactor<1.0)
momentumEquationOptions: <linearSolver=SGS,relaxationFactor=0.5,maxIterations=5>

// Pressure equation
pressureCorrectionEquationOptions: <linearSolver=PETSC,relaxationFactor=0.1,maxIterations=50>
pressureBasedMethod: SIMPLEC

// Energy equation (linearSolver[SGS,PETSC],0.0<relaxationFactor<1.0)
energyEquationOptions: <linearSolver=SGS,relaxationFactor=0.5,maxIterations=5,form=temperature>

// Turbulence equation
turbulenceEquationOptions: <model=menterSST2003, linearSolver=SGS, relaxationFactor=0.5, maxIterations=5>
kFreestream: 0.00097
omegaFreestream: 5091
eddyViscosityLimit: 10000

// Printing, plotting and restart parameters.
print_freq: 250
plot_freq: 2000
plot_output: a, pResidualTT, laminarViscosity, viscosityRatio, k, omega
restart_freq: 2000
}

Boundary Conditions

All boundary condition entries remain the same except for the inlet boundary, where one must now specify inlet values for the turbulent kinetic energy, k, and either the turbulent dissipation, epsilon, or the specific turbulent dissipation, omega. Since we are using a model in the k-omega family for this example, omega must be provided.

The boundary condition used for the inflow in this turbulent example is the subsonicInlet. This boundary condition is like the one used for compressible flows with the addition of turbulence parameters. See the following Appendix for more information about this boundary condition.

BC_3=subsonicInlet(T=537.0 R, v=41.7096 m/s, k=0.00097, omega=5091)

The boundary condition requires two turbulence parameters, k and omega`. The choice of turbulence inputs depends on the model that is selected in the turbulenceEquationOptions variable. More details can be found in the Appendix regarding the turbulenceEquationOptions variable. The outlet is a fixedPressureOutlet with a mean pressure constraint set on it as shown below.

BC_22=fixedPressureOutlet(pMean=1.0 atm)

All solid surfaces are set to noslip(adiabatic) because of the viscous nature of the flow. The keyword adiabatic must be passed to the noslip boundary condition for compressible flow simulations. More details on the noslip boundary condition can be found in the following Appendix. The front and back (going into the page) boundaries are set to symmetry to model zero variation in the flow field in the z-direction. A small section of the domain upstream is set to symmetry near the inlet because the backward step is a canonical validation problem provided by the NASA Langley turbulence modeling resource.

Initial Conditions

In this example the initial flow is a flow of air, already in motion, with a pressure of 1 atm, a temperature of 537 Ranine, and a velocity of 41.7096 m/s, which is specified as follows:

initialCondition: <p=1 atm, T=537.0 R, v=41.7096 m/s, k=0.00097, omega=5091>

Depending on the turbulence model selected for the turbulenceEquationOptions like the options shown in the RANS options table, the name of the turbulence variable provided in the initial condition will change (will either be omega or epsilon).

Transport Properties

For this case, the fluid is air, and the viscosity and thermal conductivity are set to be constant values that are selected to model the typical values for air at the temperature and pressure of the example case under consideration. The const_viscosity value for the transport_model option allows for a single value of the viscosity and thermal conductivity to be set, as shown below.

transport_model: const_viscosity
mu: 2.498e-5
kcond: 4.175e-2

A specification of the species is needed when running compressible flows. This provides information about the equation of state to use for the species in the domain. The species information for the air is encoded in the chemistry model file (.mdl) file for this case, whose specification format can be found here. The contents of the file are reproduced here for ease of replicating this case.

The .mdl file for the air species used in the backward step case.

// Model for Air as an ideal gas
species = {
_Air = < m=28.89, n=2.5, href=0, sref=0, Tref=298.0, Pref=10000.0, mf=1.0 >;
};
reactions = {
};

Numerics

For turbulent flows, the user must set the value of the variable flowRegime to turbulent in the run control file.

flowRegime: turbulent

In Stream, the inviscid flux used for the turbulence equations may be set independently from the main inviscid flux used for the momentum, energy, and species equations by using the turbulenceInviscidFlux variable. The default value is SOU, which provides for the second-order upwinding of the independent variables k, omega and epsilon in the convection term of the turbulence equations. To achieve second-order spatial accuracy, one should use a value of SOU for both inviscidFlux and turbulenceInviscidFlux. Under certain extreme flow scenarios, convergence of the system of equations may be difficult to obtain using second-order convective fluxes for the turbulence equations, requiring one to downgrade to first-order upwinding by specifying a value of FOU for the turbulenceInviscidFlux variable. This, however, has rarely been found to be needed in practice.

The first-order accurate BDF time-stepping scheme and the second-order inviscidFlux option SOU are used is used in this example. BDF is used because the time-accurate evolution of the flowfield is not of interest, only the steady state solution is desired.

The momentum, pressure correction, energy, and turbulence closure equations need to be solved for compressible turbulent flows.

The new addition is the turbulenceEquationOptions which controls the turbulence model that is used as well as the numerical controls for solving the turbulence closure equations.

turbulenceEquationOptions: <model=menterSST2003, linearSolver=SGS, relaxationFactor=0.5, maxIterations=5>

The linear solver options are like the other governing equations that have been previously covered. All linear solvers discussed(here) are supported for the value of linearSolver, however one should rarely need to use anything other than the SGS solver.

This example uses the MenterSST2003 turbulence model, which is a Reynolds Averaged Navier-Stokes (RANS) model, because that is what the NASA validation example called for.

Output Variables

The table below shows additional field variables that are available for output in turbulent flow simulations. NOTE: The variables kClip, omegaClip and epsilonClip are boolean variables that are assigned a value of 0 for no clipping and a value of 1.0 when clipping is active. These are in addition to the field outputs that are available for the laminar compressible/incompressible simulations. Default variables are output automatically and do not need to be specified in the plot_output line in the run control file. The variables kResidualTT, omegaResidualTT, and epsilonResidualTT are useful for gauging solution convergence.

Field Variable Output for Turbulent Flows
Variable	Description	Default
k	Turbulent kinetic energy	No
kclip	Turbulent kinetic energy clipped flag	No
kResidual	Turbulent kinetic energy eq. residual	No
kResidualTT	Turbulent kinetic energy eq. turn-over time	No
omega	Specific dissipation rate	No
omegaclip	Specific dissipation rate clipped flag	No
omegaResidual	Specific dissipation rate eq. residual	No
omegaResidualTT	Specific dissipation rate eq. turn-over time	No
epsilon	Turbulent dissipation	No
epsilonClip	Turbulent dissipation clipped flag	No
epsilonResidual	Turbulent dissipation eq. residual	No
epsilonResidualTT	Turbulent dissipation eq. turn-over-time	No
viscosityRatio	Turbulent/laminar viscosity ratio	No
eddyViscosity	Turbulent viscosity	No

References

[Pope2000]

1. Pope, Turbulent Flows, Cambridge University Press, 2000.

[Hart2016]

J. Hart, “Comparison of Turbulence Modeling Approaches to the Simulation of a Dimpled Sphere,” Procedia Engineering, vol. 147, pp. 68-73, 2016.

[Stre2001]

M. Strelets, “Detached Eddy Simulation of Massively Separated Flows,” in 39th AIAA Fluid Dynamics Conference and Exhibit, Reno, 2001.

[MeKu2002]

F. R. Menter and M. Kuntz, “Adaptation of Eddy-Viscosity Turbulence Models to Unsteady Separated Flow Behind Vehicles,” in Lecture Notes in Applied and Computational Mechanics, Springer, Berlin, 2002.

[GGSM2012] (1,2)

M. S. Gritskevich, A. V. Garbaruk, J. Schütze and F. R. Menter, “Development of DDES and IDDES Formulations for the k-omega Shear Stress Transport Model,” Flow, Turbulence and Combustion, vol. 88, pp. 431-449, 2012.

[LaSp1974]

Launder, B.E.; Spalding, D.B. (March 1974). “The numerical computation of turbulent flows”. Computer Methods in Applied Mechanics and Engineering. vol. 3, issue 2, pp. 269-289

[SLSY1995]

Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z. (1995). “A new k-ε eddy-viscosity model for high Reynolds number turbulent flows”. Computers & Fluids. vol. 24, issue 3, pp. 227-238