Simulation of Laminar Incompressible Flows

The Stream solver is exceptionally suited for incompressible flows due to the use of a pressure-based solution framework. The incompressible flow assumption is appropriate for flows with low Mach number in which the density variation with pressure is minimal.

Example Case: Karman Vortex

Consider the case of an incompressible laminar viscous flow of water around a cylinder. Details about this case as well as the grid and run control files can be found on our website: https://www.snumerics.com/karman-vortex-example. In this example, a flow moving at 2.1930 \(m/s\) with a density of 1000 \(kg/m^3\) passes over a cylinder and causes a time-dependent shedding pattern of vortices behind the cylinder. This case illustrates the physical phenomenon called a Karman vortex street. A schematic of the geometry and boundaries of the case is shown in the figure below.

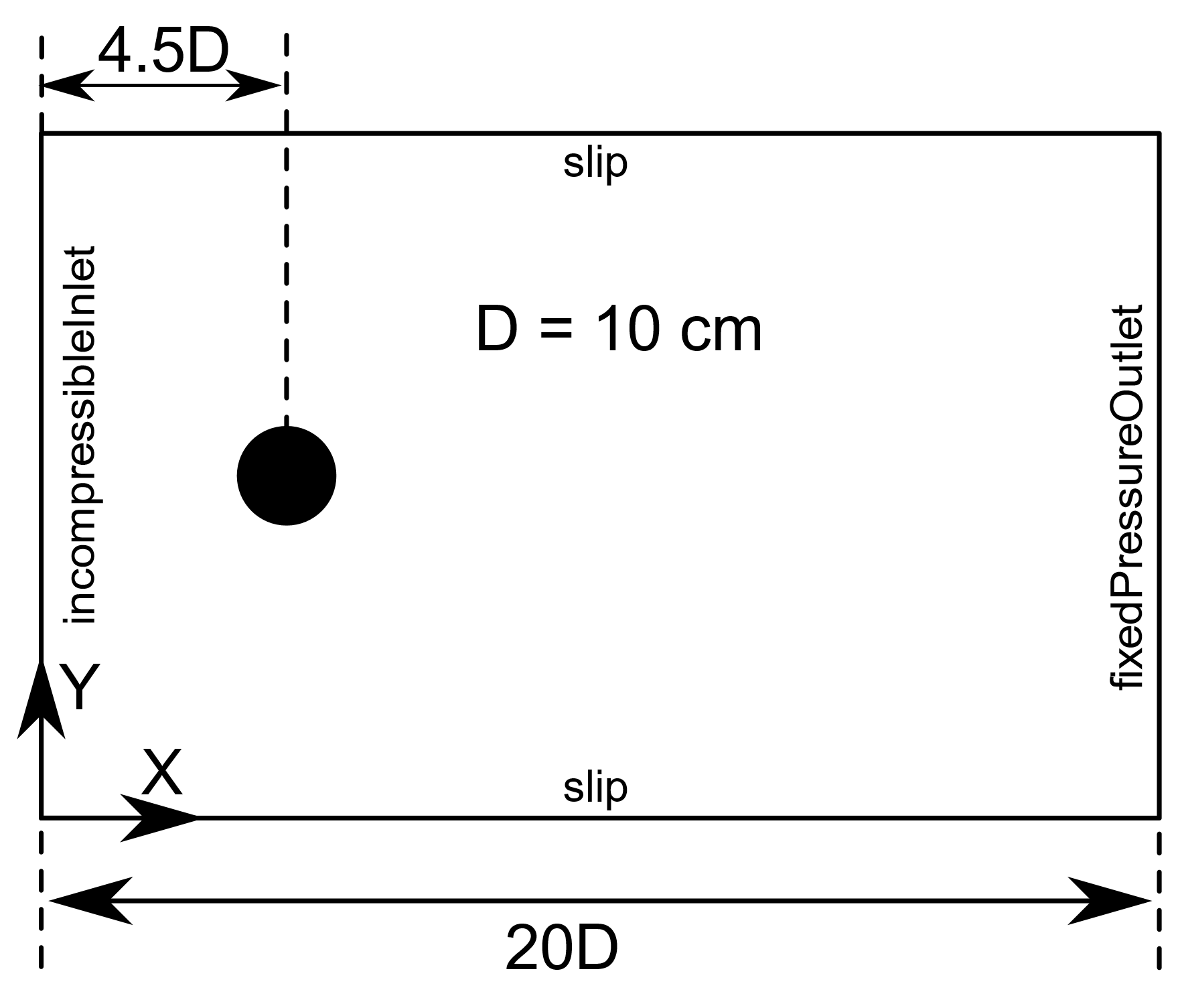
Domain diagram for the Karman vortex case.

The run control file used for this simulation is shown below.

Sample run control file for the Karman vortex case.

 {
 // Grid file information.
 grid_file_info: <file_type=VOG, Lref=1 m, pieSlice>

 boundary_conditions: <
 Inlet=incompressibleInlet(v=2.1930 m/s),
 Outlet=fixedPressureOutlet(p=1 Pa),
 Walls=slip,
 Particle=noslip,
 BackWall=symmetry,
 FrontWall=symmetry
 >

 // initial conditions in nozzle
 initialCondition: <rho=1000 kg/m^3, p=1 Pa, v=0.0 m/s>

 // Flow properties
 flowRegime: laminar
 flowCompressibility: incompressible

 // Transport properties
 transport_model: const_viscosity
 mu: 8.77205e-4

 // Time-stepping (timeIntegrator[Euler,PISO])
 timeIntegrator: BDF2
 timeStep: 1.0e-2
 numTimeSteps: 501
 convergenceTolerance: 1.0e-30
 maxIterationsPerTimeStep: 30

 // InviscidFlux [FOU,SOU,Roe(compressible only)]
 inviscidFlux: SOU

 // Gradient limiting.
 limiter: venkatakrishnan

 // HYPRE solver parameters
 linearSolverTolerance: 5.0e-02
 hypreSolverName: AMG

 // Momentum equation (linearSolver[SGS,PETSC],0.0<relaxationFactor<1.0)
 momentumEquationOptions: <linearSolver=SGS, relaxationFactor=0.7, maxIterations=3>

 // Pressure equation
 pressureCorrectionEquationOptions:<linearSolver=HYPRE, relaxationFactor=0.2, maxIterations=20>
 pressureBasedMethod: SIMPLEC

 // Printing, plotting and restart parameters.
 print_freq: 10
 plot_freq: 1
 plot_output: pResidualTT
 restart_freq: 200
 }

Boundary Conditions

The boundary condition used for the inflow in this case is the incompressibleInlet. Only the velocity on this boundary needs to be specified. The velocity specification can take many forms, many of which are described here. A velocity directed into a domain normal to a boundary can be specified by simply providing the v= input option.

Inlet=incompressibleInlet(v=2.1930 m/s)

For incompressible simulations the only boundary condition that can be used is the fixedPressureOutlet. A fixed static pressure along the boundary is set in this case. Other options for this boundary condition are detailed here. The boundary is intentionally placed far from the cylinder in a location where specifying a fixed pressure will not adversely affect the flow near the cylinder.

Outlet=fixedPressureOutlet(p=1 Pa)

The meaning of pressure in incompressible flows is not intuitively obvious. The governing equations for incompressible flow do not demand the specification of a pressure reference; only the gradient of the pressure is of importance. However, when using the fixedPressureOutlet boundary condition, the reference pressure will be set at the boundary using the value provided from the p= input option.

The boundary condition on the cylinder surface is set to noslip to enforce the zero-velocity condition. Since we are not concerned with the boundary layer effects on the upper and lower walls, the boundary condition for these boundaries is set to slip. The front and back (going into the page) boundaries are set to symmetry to model zero variation in the flow field in the z-direction.

Initial Conditions

In this example the initial flow is a quiescent flow of water with a pressure of 1 Pascal and a density of 1000 \(kg/m^3\) , which is specified as follows:

initialCondition: <rho=1000 kg/m^3, p=1 Pa, v=0.0m/s>

For incompressible simulations one should always initialize the pressure in the domain to the same value as the fixedPressureOutlet to prevent the development of large velocities at the boundary due to a discontinuous change in the pressure level.

Numerics

The second-order accurate timeIntegrator option BDF2 is chosen over the first-order accurate BDF option for this simulation since we are concerned with time accuracy. The BDF2 time-stepping scheme achieves time-accurate results at much larger timesteps compared to the BDF scheme. The second-order inviscidFlux option SOU selected here is generally preferred over FOU due to its lower numerical dissipation characteristics and should always be used if possible. Here we are using the Venkatakrishnan limiter to limit the second order convective fluxes; more information about the flux limiters can be found here.

For incompressible flows, only the momentum and pressure-correction equations need to be solved. The specification for the momentum equation options is shown below. Here we are using the symmetric Gauss-Seidel (SGS) method to solve the linear system. A relaxation factor of 0.7 has been chosen, which indicates the 70% of the current iteration solution and 30% of the previous iteration solution will be averaged and used as the new value. Lower values for the relaxationFactor can be used if numerical stability issues arise. The maxIterations option specifies the maximum number of iterations to use in the linear solver. For the SGS solver, the maximum number of iterations is always used. Typically, one should not use more than 5 iterations in the linear solver for the momentum equation.

momentumEquationOptions: <linearSolver=SGS, relaxationFactor=0.7, maxIterations=3>

Options for pressure-correction equation are shown below. The HYPRE linear solver is generally the preferred linear solver for the pressure-correction equation due to the Poisson-like nature of this equation. Typically, more iterations are required for the pressure-correction equation than the other governing equations.

pressureCorrectionEquationOptions:<linearSolver=HYPRE, relaxationFactor=0.2, maxIterations=20>

Stream supports both the SIMPLE and SIMPLEC pressure-based methods, the selection of which is made using the pressureBasedMethod variable.

pressureBasedMethod: SIMPLEC

Miscellaneous

In Stream, the method of constraining a flow to be two-dimensional is to provide the pieSlice input in the grid_file_info section. This disables the z-component of the equations. It is important to note that this option presumed a grid that exists in an x-y plane.

Helpful Guidance

• Residuals are output to the log file (lines that start with R:). These lines contain the residuals for each of the governing equations being solved. See the following Appendix for more information. A two to three order of magnitude drop in the residuals from the starting to the ending iteration within every timestep is generally considered acceptable for a time-accurate simulation.

• The table below shows the field variables that are available for output in laminar incompressible flow simulations. Default variables are output automatically and do not need to be specified in the `plot_output line in the run control file. The variables pResidualTT and vResidualTT shown in the table are useful for gauging solution convergence. A discussion of the principle behind the turn-over time can be found here.

Field Variable Output for Laminar Incompressible Flows

Variable	Description	Default
laminarViscosity	Fluid viscosity	No
pg	Gauge pressure	Yes
pPrime	Pressure-correction	No
pResidual	Pressure-correction eq. residual	No
pResidualTT	Pressure-correction eq. turn-over time	No
r	Density	Yes
v	Velocity	Yes
vort_mag	Vorticity magnitude	No
vResidual	Velocity eq. residual	No
vResidualTT	Velocity eq. turn-over time	No